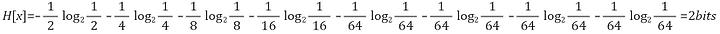정보 이론 - Information Theory
불확실성에 대한 일어날 가능성을 모델링하는 것이 Probability Theory라고 하고, 이런 불확실한 상황에서 추론에 근거해 결정을 내리는 것을 Decision Theory라 합니다.
그렇다면 Information Theory는 이러한 불확실성을 평가하는 것이라고 정의할 수 있습니다.
먼저 Information Theory에 대한 기본 개념을 쉽게 이해하기 위해서 aistudy.co.kr에 있는 예제를 기반으로 설명해 보도록 하죠..
다음과 같이 가로, 세로 4장씩의 카드가 놓였다고 할 때, 여러분이 한 장의 카드를 선택했다고 해 보죠.
다음과 같은 질문 과정을 거쳐서 선택한 카드를 맞출 수 있습니다.
상단에 있습니까?
예
그럼 상단의 오른쪽 반에 있습니까?
아닙니다.
그럼 왼쪽 반의 상단에 있습니까?
아닙니다.
그럼 왼쪽 반 하단의 오른쪽에 있습니까?
그렇습니다.
당신이 선택한 것은 크로바 3입니다.
여기에서 알 수 있는 사실은 16장의 카드가 있을 때, 선택한 카드를 맞힐 확률은 1/16입니다.
그리고 카드를 맞추기 위한 질문의 회수는 4회입니다.
즉, 이를 수치로 표시하면 다음과 같이 나타낼 수 있겠죠.
엔트로피 (Entropy)
어떤 확률변수의 불확실성을 측정하는 것을 바로 엔트로피라고 합니다.
엔트로피는 Claude Shannon이 이야기 한 것으로 정보량을 나타내는데요.
위 예에서 보면 4번의 질문으로 불확실성을 해결했으므로 엔트로피는 4라고 할 수 있습니다.
이러한 엔트로피 h(x)를 구하는 공식은 다음과 같습니다.
확률 p(x)에 log를 취하는 것은 바로 p(x)를 표시할 수 있는 자리 수(bit)를 나타낸다고 할 수 있습니다.
음수를 취하는 이유는 확률 p(x)가 1보다 작기 때문에 log를 취하면 음수가 됩니다.
그러므로 계산하기 편하도록 양수로 변경하기 위해 적용한 것이라고 보면 됩니다.
그렇다면 확률분포에 대한 기대값을 계산하는 방식으로 p(x)를 표시할 수 있는 공간을 나타내는 엔트로피를 계산해보면 다음과 같습니다.
어떤 랜덤 변수 x가 8가지의 상태가 동일한 확률로 발생한다고 할 때, 엔트로피는 다음과 같이 계산할 수 있습니다.
즉, 3bit의 데이터를 가지고 x가 발생할 확률을 모두 표현할 수 있다는 것입니다.
만약 8개가 발생할 확률이 동일하지 않다면 어떻게 될까요?
만약 8개의 확률이 다음과 같이 다양하다고 할 때, 엔트로피를 계산해 보도록 하죠.
이렇게 불균형한 분포를 보일 경우 엔트로피가 더 작아지는데, 우리가 예측해서 맞출 수 있는 확률이 더 높아졌기 때문에 정보의 양 즉 엔트로피가 더 작아진 것입니다.
반대로 생각하면 불확실성이 높아질 경우, 정보의 양은 더 많아지고 엔트로피는 더 커진다고 할 수 있습니다.
최대 엔트로피 계산
기계학습과 관련된 수학을 공부하다보면 최대 또는 최소값을 계산하는 것이 중요한 경우가 많습니다.
예전에 Maximum likelihood를 계산할 때, 미분해서 0이 되는 값으로 최대값을 구한다고 이야기했었습니다.
그런데 특정 condition이나 constraints에 종속되는 함수의 최대, 최소값을 찾는 것은 보다 어려운 면이 있습니다.
이럴 때, Lagrange Multipler를 사용해서 condition을 분명하게 해결하고 여분의 변수를 제거함으로써 이런 문제를 풀어 낼 수 있다고 합니다.
여기서는 확률의 총합이 1이라고 하는 Constraint가 있다고 보고 다음과 같이 최대값을 구할 수 있습니다.
우측에 있는 p(x)의 합에서 1을 뺀 값이 0이 되는 것이 확률의 기본 조건이므로
해당 부분을 Lagrange Multiplier로 표시한 것을 알 수 있습니다.
이제 이 수식을 두번 미분해서 원하는 최대 엔트로피를 구할 수 있다고 합니다.
앞서 설명했듯이 모든 확률이 똑같은 경우에 엔트로피는 최대가 되겠죠..
만약 연속확률분포에서의 엔트로피를 구한다면 다음과 같이 적분을 이용해서 구할 수 있겠죠.
한가지 재미있는 사실이 Lagrange Multiplier를 적용해서 위 수식에서 엔트로피를 최대로 만드는 확률 p(x)를 구해보면 다음과 같다고 합니다.
어디서 많이 본 수식 아닌가요?
바로 정규분포를 나타내는 Gaussian distribution과 동일한 것입니다.
상대적인 엔트로피 (Relative Entropy)
확률분포 p(x)를 모를 때, 모델링을 통해 q(x) 확률을 가정해서 사용할 수 있습니다.
이런 경우 가정한 q(x)의 정확성을 확인하기 위해 정보를 표현하는 공간의 차이를 계산해서 확인할 수 있습니다.
이것을 상대적 엔트로피 (Relative Entropy) 또는 Kullback-Leibler divergence라고 합니다.
여기서 Convex 함수에 대해서 살펴보도록 하죠.
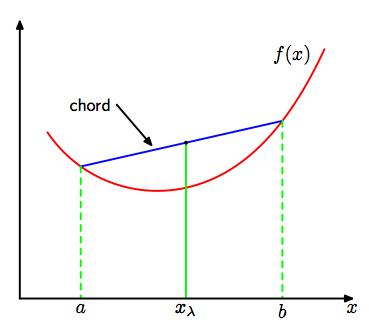
Convex 함수는 아래 그림과 같은 형태로 a, b의 평균보다 f(a), f(b)의 평균이 더 큰 것을 의미합니다.
즉, Convex 함수는 다음과 같은 성격을 가지고 있다고 할 수 있습니다.
개별적인 a와 b의 평균보다 f(a)와 f(b)의 평균이 더 크다는 것을 나타내고 있습니다.
이와 반대의 함수를 Concave라고 합니다.
일반적으로 log함수는 Concave 형태를 나타내는데요.
엔트로피를 구하기 위해서는 - (음수)를 취했기 때문에 Concave가 Convex가 되므로 위 공식을 적용할 수 있게 됩니다.
위 공식을 기대값에 적용해 보면 다음과 같습니다.
이를 relative entropy에 적용하면 다음과 같다고 하네요.
마치면서
마지막으로 엔트로피를 이용한 Information Theory는 기계학습, 정보검색, 자연어 처리 등에서 많이 활용되고 있습니다.
예를 들어, 정보검색에서는 문서와 질의어를 확률변수로 모델링하고 이 모델간의 거리를 바탕으로 문서의 랭킹을 계산하는데,
이때 사용되는 척도가 정보이론에서 제공된다고 합니다.
또한 압축이나 연관성 분석에도 엔트로피의 활용이 높다고 하네요.
이상으로 엔트로피와 관련된 Information Theory에 대해서 정리했습니다.
추가적인 내용은 향후 필요할 때 더 정리하도록 하죠.