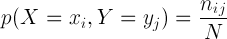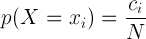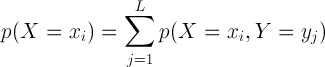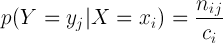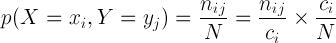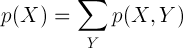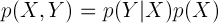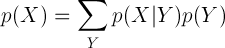확률 이론 - Probability Theory

기계학습에서 많이 사용하는 확률 이론에 대해서 살펴보도록 하겠습니다.

확률과 관련해서 처음 볼 경우에는 확률 - 일어날 가능성을 측정하는 방법 을 읽어보면 기본 개념을 이해할 수 있습니다.

여기에서는 비슷한 내용이기는 하지만 다른 방향에서 살펴보도록 하죠.. 

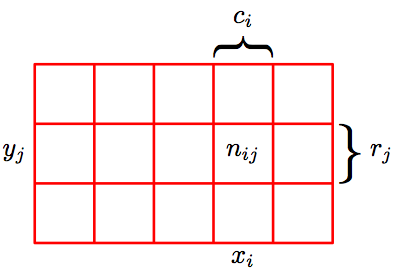
다음 그림에서 전체 갯수가 N이라고 할 때, 임의의 값 x와 y가 동시에 나올 확률은 어떻게 될까요? 

x와 y가 동시에 나오는 경우를 전체 갯수로 나누면 되겠죠. 

보통 동시에 나올 확률을 교집합으로 표기하기도 하는데, "Pattern Recognition and Machine Learning"에서는 다음과 같이 표시하네요. 

이어서 임의의 x가 나올 확률은 다음과 같이 표시할 수 있습니다. 

위 그림을 잘 살펴보면 직관적으로 확인할 수 있을 것입니다. 

두 수식을 함께 보면 P(X)의 확률은 P(X,Y)의 확률에서 모든 Y축의 확률을 더하면 된다는 것을 알 수 있습니다. 

이를 수식으로 표현하면 다음과 같습니다. 

이것을 "sum rule"이라고 하는데요. 즉, X는 그대로 두고 Y의 모든 확률을 더한 것이라고 해석할 수 있습니다. 

이어서 조건부 확률(Conditional Probability)을 한번 살펴보도록 하죠. 

X가 일어난 상황에서 Y가 발생할 확률을 조건부 확률이라고 하는데요. 

처음 그림을 보면 다음과 같이 나타낼 수 있습니다. 

이제 맨 처음 살펴본 x와 y가 동시에 나올 확률에 이 수식을 적용해 보죠.. 

이 수식을 "product rule"이라고 합니다. 

베이즈정리에서도 계속 활용하게 되므로 잘 알아두면 좋을 듯 합니다. 

두 수식을 다시 한번 정리해 보면 다음과 같습니다. 

sum rule

product rule

마지막으로 두 수식을 연결하면 다음과 같은 공식도 만들어 낼 수 있습니다. 

sum rule의 p(X,Y) 대신 product rule을 삽입하면 나오는 식입니다. 

그리고 product rule에서 X와 Y가 서로 독립이라고 가정하면 

p(Y|X)는 X에 아무런 영향을 받지 않기 때문에 P(Y)라고 할 수 있습니다. 

그래서 X, Y가 서로 독립일때는 다음과 같은 공식이 성립합니다. 

이상으로 기본적인 확률에 대해서 살펴봤습니다. 

위에서 정리한 sum rule과 product rule을 기계학습에서 어떻게 활용하는지 앞으로 확인하도록 하죠..