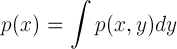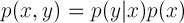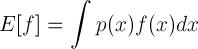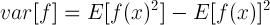Probability Density

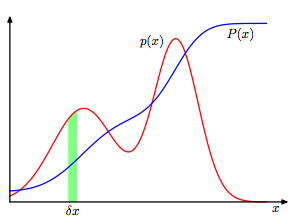
연속 함수는 다음과 같은 그림으로 나타낼 수 있습니다.

연속 함수의 확률을 구하기 위해서는 각 구간을 조그맣게 자르고 그 간격을 δx라고 표시합니다.

그리고 연속함수의 임의의 변수 x가 (x, x+δx)에 있다고 할 때, 변수 x가 나올 확률은 p(x)δx로 표시할 수 있습니다.

최종적으로 (a, b) 구간 사이에 변수 x가 있을 확률은 위에서 구한 p(x)δx를 모두 합하면 됩니다.

연속함수이므로 이러한 합을 구하는 것은 바로 적분을 사용하면 됩니다.

확률이므로 p(x)는 0보다 크고 모든 확률의 합은 1이 됩니다.

연속 확률에서도 Sum Rule과 Product Rule을 다음과 같이 정리할 수 있습니다.

Sum Rule

Sum Rule에서 합을 나타내는 Σ를 적분으로만 바꾼 것으로 생각하면 됩니다.

보통 기대값(Expectation)은 p(x)의 확률로 나타나는 어떤 함수 f(x)의 평균을 이야기합니다.

그래서 이산분포에서는 다음과 같이 확률(p(x)과 함수값(f(x)를 곱해서 모두 더하면 됩니다.

연속 분포에서는 합을 구하기 위해서 적분을 하면 되겠죠.

평균을 구한 다음 평균에서의 거리 즉, 분산을 계산하기 위해서는 (값-평균)을 제곱하면 됩니다.

즉, 다음과 같이 f(x)에 대한 분산을 계산할 수 있습니다.

분산이므로 f(x)가 기대값 E[f(x)] 주변에 어떻게 분포되어 있는지를 알 수 있겠죠.

계산을 쉽게 하기 위해 위 식은 다음과 같이 나타낼 수도 있습니다.

잘 이해가 안되면 이전에 작성한 이산확률분포 - 기대 수준을 관리를 참고해도 좋을 듯 합니다.

이외에도 covariance라고 임의의 두 변수 x와 y가 있을 때 분산을 계산하는 것이 나오는데요.

x가 증가할 때 y가 증가하거나 감소한다면, x와 y는 선형 관계에 있다고 할 수 있을 것입니다.

반대로 서로 관계가 없다면 covariance는 0이 되겠죠.. 이런 경우를 독립 관계라고 합니다.