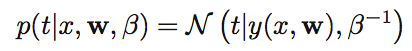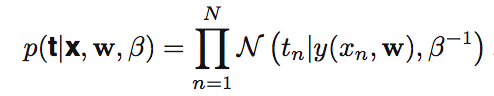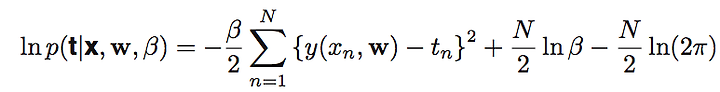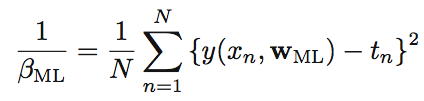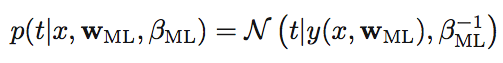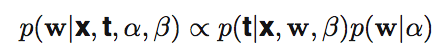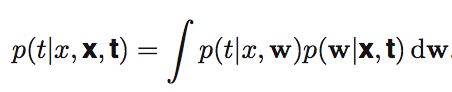Curve Fitting으로 살펴보는 Frequentest와 Bayesian Treatment

이전에 살펴본 베이즈 확률(Bayesian Probabilities)과 가우스 분포(Gaussian Distribution) 에서 Frequentest와 Bayesian에 대해서 정리를 했었습니다. 

실제 Curve Fitting에서 이 두가지 방식이 어떻게 적용되는지 살펴보도록 하죠. 

Curve Fitting에 대해서는 기계학습 첫 강좌에서 설명했었습니다. 

주어진 입력값 x에 대한 타겟을 t라고 했을 때, x에 대응하는 값 y(x, w)에 대해 다음과 같은 관계가 성립한다고 합니다. 

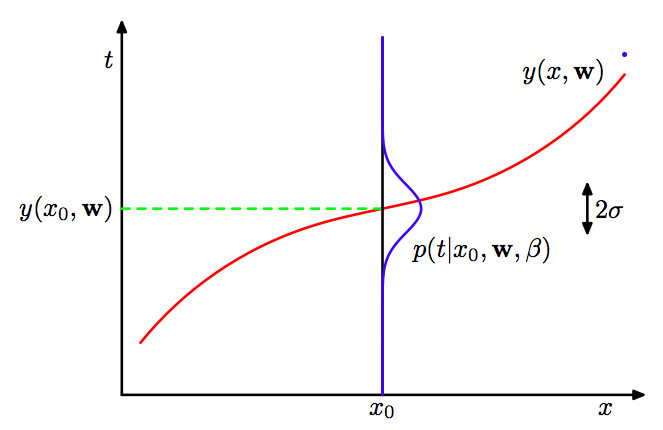
다음 그림을 옆으로 보면 y(x,w)에 대해 정규 분포의 형식을 가지고 있는 것을 알 수 있습니다. 

정규분포를 따르므로 y(x,w)는 평균,  β−1은 분산이 된다는 것을 알 수 있습니다. 

앞서 정리한 가우스 분포(정규 분포)에 대한 수식과 비교해 보면, 왜 평균 분산이 되는지 알 수 있을 것입니다. 

이제 임의의 x와 t에 대한 Curve Fitting을 결정하기 위해서 w와  β를 최대로 하는 maximum likelihood를 구해야 합니다. 

이것이 바로 Frequentest Treatment라고 하는 방법입니다. 

각각의 y(x,w)는 독립이므로 모두 곱해주면 확률을 구할 수 있겠죠. 

가우스 분포에서 평균과 분산에 대한 maximum likelihood를 구했던 것을 생각해보면 똑같은 방식으로 구할 수 있을 것입니다. 

먼저 log를 취해서 maximum likelihood를 계산하기 편하게 합니다. 

log를 취하더라도 최대, 최소값은 변경되지 않기 때문입니다. 

위식은 정규분포의 기본 공식에 log를 취해서 만들어진 식이 됩니다. 

Maximum likelihood를 구하기 위해서 위 식을 미분해서 0이 되는 값을 구하면 바로 최대값을 알게 됩니다. 

이렇게 하면 다음과 같은 식을 구하게 됩니다. 

w와 β에 대한 maximum likelihood를 알고 있으므로 확률을 계산할 수 있게 되겠죠. 

이렇게 구하는 maximum likelihood의 단점은 동전을 세번만 던져서 모두 앞면이 나왔다면, 

앞면이 나올 확률을 1로 보고서 maximum likelihood를 계산하기 때문에 잘못된 결과가 나오게 됩니다. 

즉, 시도한 회수가 작거나 반복적으로 실행해 볼 수 없는 경우 Frequentest는 문제가 될 수 있다는 것이죠. 

그래서 이런 경우 대안으로 Bayesian Treatment를 사용하게 됩니다. 

Bayesian에서는 x와 t를 가지고 w를 확률에 따른 값으로 보고서 계산을 하는 것으로 maximum likelihood가 아닌 w를 가정해서 활용하게 됩니다. 

Bayesian의 표현을 통해서 위의 curve fitting에 적용하면 다음과 같습니다. 

복잡하니 α와 β를 제외하고 Bayesian 공식으로 정리해보면 다음과 같습니다. 

Bayesian Treatment는 계산이 복잡하기는 하지만 Frequentest의 단점을 보완하기 때문에 많이 사용한다고 합니다. 

이러한 공식을 통해서 다음과 같은 curve fitting을 그려낼 수 있습니다.

마지막으로 The Curse of Dimensionality에 대해서 간단히 정리하고 마치려고 합니다. 

기계학습에서 Dimension이 늘어나면 처리해야 할 양이 지수승으로 증가하게 됩니다. 

그래서 계산량이 늘어나고 쏠림현상이 발생해서 잘못된 결과를 예측하게 되는 경우가 많은데요. 

이를 Dimension의 저주라고 합니다. 

The Curse of Dimensionality를 피하기 위해서는 먼저 Dimension을 줄이고, 변수를 너무 많이 사용하지 않도록 해야 한다고 합니다. 

다음에는 Decision Theory와 Information Theory에 대해서 정리해 보도록 하겠습니다.