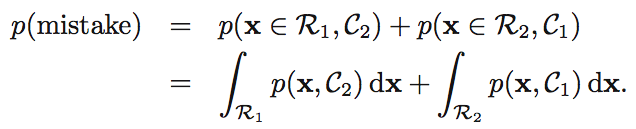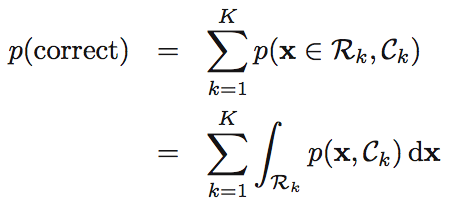의사결정이론 - Decision Theory
앞에서 확률이론과 Bayesian & Frequentist에 대해서 살펴봤습니다.
기계학습의 목표는 이러한 이론들을 활용해서 주어진 입력값 x에 대한 타겟인 t를 예측하는 것이었습니다.
불확실성에 직면해서 결정을 내려지 않으면 안될 경우, 어떤 결정을 해야 하고,
어떤 정보를 이용해야 하는지에 대해서 다루는 것이 바로 의사결정이론 (Decision Theory)입니다.
Decision Theory
병원에서 암을 진단하기 위해 X-ray 사진이 주어졌다고 생각해 봅시다.
X-ray 사진을 보고 암에 걸렸는지 아닌지 결정해야 할때, Decision Theory를 활용할 수 있습니다.
암일 경우를 클래스 1(C1)이라고 하고, 암이 아닌 경우를 클래스 2(C2)라고 할 때,
주어진 X-ray 사진(x)이 특정 클래스에 들어갈 확률은 베이즈 정리를 활용해서 다음과 같이 쓸 수 있습니다.
베이즈 확률에서 이야기 한 Posterior, Prior, Likelihood의 관계를 항상 생각하시기 바랍니다.
병원 예제에서는 X-ray 사진(x)이 잘못된 클래스로 할당되어 오진이 발생할 경우를 최소화해야 하므로,
상대적으로 높은 Posterior 확률을 가진 것을 선택해야 합니다.
이것이 바로 Decision Theory입니다.
오류(misclassification rate) 최소화
위의 X-ray 예제에서 오진할 확률은 환자가 암에 걸리지 않았는데 암에 걸린 것으로 진단하거나 반대의 경우라고 할 수 있습니다.
C1, C2 클래스로 진단했을때, 실제 영역을 R1, R2라고 하면 다음과 같이 오류가 발생할 확률을 구할 수 있습니다.
반대로 정확하게 결정할 확률은 주어진 x에 대해 R1, C1 / R2, C2가 일치하는 경우가 되겠죠.
여기에서도
가 되고, p(x)가 모든 요소에 대해 공통적인 요소이므로,
각각의 x가 가장 높은 Posterior 확률을 갖는 클래스에 할당된다는 것을 다시 한번 확인 할 수 있습니다.
기대손실(expected loss) 최소화
X-ray 사진으로 암여부를 잘 못 진단했을 경우를 생각해 보죠.
실제 암이었는데 정상이라고 오진한 경우가 그 반대보다 더 큰 실수가 될 것입니다.
이러한 상황에 따른 패널티 또는 가중치를 두고서 결정을 해보자는 것이 바로 기대손실 최소화 입니다.
즉, 잘못된 결정에 따른 피해를 가장 적게 하는 방향으로 결정을 해보자는 데서 출발한 것이지요.
이를 위해 다음과 같은 행렬(L)을 만들고 패널티를 부여합니다.
1000이 주어진 경우가, 실제 암(R1)인데 정상인 클래스(C2)에 할당한 것이 됩니다.
이것을 수식으로 나타내면 기존 확률에 위의 패널티를 곱해주게 됩니다.
rejection option
의사 결정이 어려운 상황일 때, 의사결정을 피하는 것이 적절한 경우가 있습니다.
한계점(threshold)을 지정해서 이러한 영역을 제외하는 것을 rejection option이라고 합니다.
다음 그림을 보면 reject region에 해당하는 영역에서는 클래스에 할당하는 결정을 하지 않는다는 것이죠.
추론과 의사결정
의사결정 이슈를 해결하기 위해 먼저 추론(inference)을 해야 하는데 다음과 같은 접근법이 있습니다.
1. 베이즈 정리 활용
앞에서 설명한대로, 주어진 x에 대해 어느 클래스에 할당될 확률이 높은지 계산하면 의사결정을 할 수 있게 됩니다.
즉, Posterior를 계산하는 것이 Decision Theory에서 중요한 부분이 되는 것이죠.
이것을 베이즈 정리를 통해서 계산해 낼 수 있습니다.
2. Posterior를 직접 계산
두번째 방식으로는 Posterior를 베이즈 정리를 활용하지 않고 직접 계산하는 것입니다.
를 바로 계산해서 주어진 x가 어느 클래스에 들어갈지를 결정하는 것이죠.
3. 판별식 함수(discriminant function) 활용
마지막으로 확률을 이용하지 않고, 특정 함수를 이용해서 결정하는 방식입니다.
discriminant function이라고 하는 f(x)가 있을 때,
f = 0이면 클래스 1로 결정하고, f = 1이면 클래스 2로 결정하는 방식입니다.
회귀분석에서의 Loss function
다음 그림을 보면 파란선은 정규분포를 따르고 있습니다.
그리고 파란선의 평균값인 E[t|x]가 바로 y(x)값이 된다는 것도 알 수 있습니다.
또한, y(x)와 t의 차이가 적을 수록 오류가 최소화된다는 것을 확인할 수 있습니다.
그러므로 손실함수(Loss function)을 다음과 같이 나타냅니다.
책에서는 이 Loss function으로부터 y(x)와 E[t|x]가 같다는 것을 증명하는 것이 나와 있습니다.
어쨌든 그림에서 어느정도 이해할 수 있으므로 생략하도록 할께요. (수식 대입하고 미분해서 0이 되는 값을 구하는 형식입니다.)
분명히 알아야 할 점은 오차의 분포가 정규분포인 경우, 이러한 Loss function이 가장 효율적이라는 점입니다.
제곱을 하기 때문에 이것을 square loss 라고 하기도 합니다.
이상으로 Decision Theory에 대해 정리해 봤습니다.
다음에는 엔트로피와 관련된 Information Theory를 간략하게 정리해 보겠습니다.