컴퓨터공학/통계학

통계적 가설 검정(Statistical Hypothesis Testing) 절차

미니~ 2017. 3. 13. 08:16

통계적 가설 검정은 통계적 추측의 하나이다.

전체 집단의 실제 값이 얼마라는 주장에 대해서 표본을 활용해 가설의 합당성 여부를 판단하는 것이다.

빅데이터 시대에는 전체 데이터 대상으로 수집, 처리하기 때문에 통계적 가설 검정이 필요하지 않다.

그러나 전체 데이터를 수집할 수 없다면, 통계적으로 가설이 적합한지를 결정하기 위해 반드시 필요한 절차다.

통계적 가설 검정 절차

통계적 가설 검정은 다음 5가지 절차를 거쳐서 수행한다.

1. 유의수준의 결정, 귀무가설과 대립가설 설정

2. 검정통계량 결정

3. 기각역의 설정

4. 검정통계량 계산

5. 통계적인 의사결정

유의수준의 결정, 귀무가설과 대립가설 설정

유의수준(Significance level)이란 통계적 가설 검정에서 사용하는 기준값으로 $\alpha$ 로 표시한다.

여론조사 등에서 주로 사용하는 신뢰도 95%라고 할 때, 유의수준은 (1-0.95)로 계산해서 0.05가 된다.

보통 유의수준과 유의확률(Significance Probability, p-value)을 비교해 통계적 유의성을 검정하게 되는데

p-value에 대해서는 아래에서 정리하기로 한다.

통계적 가설은 귀무가설( $H_{0}$ )과 대립가설( $Ha$ )로 나누어진다.

우리나라 남성의 평균 키가 180cm라는 가설을 검정한다고 가정해보자.

이때 귀무가설은 다음과 같이 표기할 수 있다.

$H_{0}$ : $\mu =180$

그리고 이에 대한 대립가설은 먼저 180cm가 아니라고 설정할 수 있다.

$H_{1}$ : $\mu \neq 180$

위와 같이 대립가설은 양측검정(two-sided test)을 해야 한다.

즉, 가설검정에 대한 기각영역이 180보다 작은 부분과 큰 부분으로 양쪽에 있게 된다.

그래서 유의수준도 $\alpha$ /2로 계산하게 된다.

반면에 다음과 같은 대립가설을 설정할 수도 있다.

$H_{1}$ : $\mu >180$

이와 같이 기각영역이 한쪽에만 있는 경우를 단측검정이라고 한다.

검정통계량 결정 및 계산

검정통계량은 가설 검정에서 전체 데이터를 사용할 수 없기 때문에 이용하는 표본 데이터의 통계량을 말한다.

보통 검정통계량은 정규분포, t분포, x2분포, F분포의 확률분포에 따라 통계량을 구한다.

검정통계량을 구하는 공식은 다음과 같다.

정규분포 t분포 x2분포 F분포

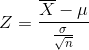
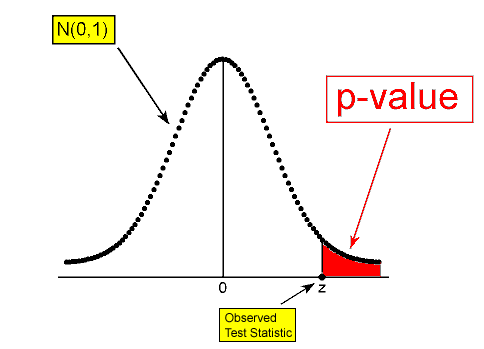
한가지 주의할 점은 검정통계량은 확률 값을 구하는 것이 아니라 그래프의 x축 좌표를 구한다는 것이다.

아래 그림을 살펴보면 정규분포(z)에 따른 검정통계값을 "Observed Test Statistic"이라고 표시하고 있다.

이 그림에 보면 p-value가 등장한다.

p-value는 귀무가설이 맞다는 전제하에 통계값이 실제로 관측된 값 이상일 확률을 의미한다.

따라서 p-value가 너무 낮다면 그렇게 낮은 확률이 실제로 일어났다고 생각하기 보다는 귀무가설이 틀렸다고 생각하게 된다.

그래서 귀무가설을 기각하고 대립가설을 채택하게 된다.

일반적으로 p-value가 0.05 또는 0.01보다 작으면 귀무가설을 기각하는 것이 관례이다.

아래 기각역의 설정과 비교해서 살펴보면 유의수준과 유의확률(p-value)을 조금이라도 이해할 수 있을 것이다.

기각역의 설정

앞에서 유의수준 $\alpha$ 를 계산했는데 이 영역에 포함될 경우, 귀무가설을 기각하고 대립가설을 채택하게 되므로 기각역(Critical Region)이라고 한다.

반대로 1- $\alpha$ 영역은 귀무가설을 채택하게 되기 때문에 채택역(Acceptance Region)이라고 한다.

앞서 계산한 검정통계량이 x축 좌표라고 했는데, 이 값이 어느 영역에 있는지에 따라 귀무가설을 채택하거나 기각하게 된다.

통계적 의사결정

마지막으로 통계적 가설 검정에 따른 결론을 내리는 단계이다.

만약 대한민국 남성 평균 키가 180cm라는 귀무가설에 대한 검정통계량이 채택역 안에 있다면,

"대한민국 남성의 평균 키는 180cm라고 할 수 있다" 와 같이 결론을 내리면 된다.

위 내용을 숙지하고 실제로 통계적 가설 검정을 수행하는 예제를 살펴보면 확실히 이해가 갈 것이다.