 OpenCV 이미지 유사도 비교 #2 - 히스토그램 비교
OpenCV 이미지 유사도 비교 #2 - 히스토그램 비교
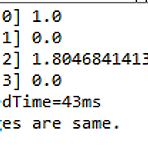
OpenCV를 활용한 이미지의 유사도 비교에서 먼저 피처 매칭을 살펴봤다. 오늘은 히스토그램 비교를 알아보도록 하자. 히스토그램은 매개변수에 따라 Correlation, Chi-square, Intersection, Bhattacharyya 각각의 결과값을 가질 수 있다. 그래서 중요한 부분이 각각의 결과값을 어떻게 해석하는 것이다. Correlation과 Intersection은 값이 클수록 유사한 것이고, Chi-square와 Bhattacharyya는 값이 작을수록 유사한 것으로 판단한다. Comparing Histogram 먼저 전체 소스를 살펴보면 다음과 같다. 마찬가지로 C로 구현되어 있는 Histogram 소스를 자바로 변환한 것이다. package kr.co.acronym; import j..
 R 데이터셋 처리 함수들에 대한 간단한 정리~
R 데이터셋 처리 함수들에 대한 간단한 정리~
R을 활용하면 다양한 데이터셋을 data.frame으로 읽어서 많은 작업을 할 수 있다. 어떤 작업들이 가능한지 R에서 데이터셋을 처리하는 함수를 중심으로 살펴보기로 하자. Motor Trend Car Load Test 예제로 사용할 데이터셋은 R에 내장되어 있는 mtcars이다. 이 데이터는 1974년 Motor Trend US magazine에서 추출한 것으로 1973년, 1974년 모델의 32개 자동차들의 디자인과 성능을 비교한 것이다. help 명령어로 데이터 포맷 등을 먼저 살펴보기 바란다. > help(mtcars) 데이터셋의 정보 확인 먼저 mtcars 데이터를 가져와 보자. 데이터셋을 가져오기 위해서 간략하게 data() 함수를 호출하면 된다. > data(mtcars) 32개의 자동차의 ..
 OpenCV를 활용한 이미지 유사도 비교 방법~
OpenCV를 활용한 이미지 유사도 비교 방법~
OpenCV는 인텔이 개발한 오픈소스 컴퓨터비전 C 라이브러리이다. 실시간 이미지 프로세싱을 위한 라이브러리로 윈도우, 리눅스 등 여러 플랫폼에서 활용할 수 있다. 원래 C 언어로 되어 있지만 최근에는 Java 언어로도 적용할 수 있고, 안드로이드 및 아이폰과 같은 모바일 환경도 지원한다. 다양한 이미지 프로세싱 알고리즘을 지원하기 때문에 처음에는 두 이미지가 동일한지 비교하는 메소드 같은 것이 존재할 줄 알았다. 그러나 두 이미지의 동일성을 OpenCV로 비교하는 것은 생각보다 쉽지 않았다. 히스토그램 비교, 템플릿 매칭, 피처 매칭의 세 가지 방법이 있다고 하는데 각각의 방법으로 구현한 다음 많은 테스트를 통해 실제 어느 정도 값이 나오면 일치한다고 판단할지를 정해야 한다. 이 부분은 다음 번 글에서..
 Nonparametric Method - 평균/분산을 모를때 확률분포를 만드는 방법
Nonparametric Method - 평균/분산을 모를때 확률분포를 만드는 방법
지금까지 살펴본 확률분포는 모두 평균이나 분산과 같은 매개변수들을 기반으로 확률분포를 정하게 됩니다. 예를 들어, 정규분포(Normal Distribution)에서는 평균과 분산을 알고서 확률분포를 구하게 되죠.. 그런데 만약 평균과 분산과 같은 매개변수를 모를 경우, 확률 분포를 어떻게 알 수 있을까요? 특히 정규분포와 달리 여러개의 봉으로 이루어진 데이터라면, 기존의 방식으로 확률 분포를 알수는 없을 겁니다. 이렇게 매개변수가 없을 때, 확률 분포를 구하는 방법을 Nonparamtric Method라고 합니다. (보통 비모수적 방법이라고 이야기 하는 것 같습니다.) Nonparametric Method는 보통 Histogram, Kernel Density, Nearest Neighbour 세가지가 있..
 통계를 왜 배워야 하는가?
통계를 왜 배워야 하는가?
미분적분, 수치해석, 확률통계~ 고등학교 때부터 대학교 초기까지 배웠던 통계 관련 과목들입니다. 그동안 별로 관심을 가지지 않고 지냈었는데.. 최근 프로젝트와 맞물려서 다시 공부를 해야 겠다는 생각을 했네요. 역시 사람은 뭐든지 필요할 때가 되어야 비로소 진정한 의미를 알고 다시 시작하는 건가 봅니다. ^^ 앞으로 꾸준히 통계 부분에 대해서는 공부를 하면서 가끔 정리해 볼 계획입니다. 제가 뭐 통계학자도 아니고, 수학을 전공한 사람도 아니기에 제가 이해하는 수준에서 나중에 참고할 수 있도록 부담없이 정리하려고 합니다. 혹시 제가 잘못 이해하고 있는 것을 본 전문가들은 가감없이 댓글 달아주시면 좋겠습니다. 통계의 중요성먼저 통계가 무엇인지부터 정리를 해야 할 것 같네요. Head First Statisti..
